Last modified: July 10, 2024

This article is written in: 🇺🇸

Neural Networks Introduction

Neural networks represent a cornerstone in the field of machine learning, drawing inspiration from neurological processes within the human brain. These networks excel in processing complex datasets with numerous features, transcending traditional methods like logistic regression in both scalability and efficiency. Particularly, logistic regression can become computationally intensive and less practical with a high-dimensional feature space, often necessitating the selection of a feature subset, which might compromise the model's accuracy.

A neural network comprises an intricate architecture of neurons, analogous to the brain's neural cells, linked through synaptic connections. These connections facilitate the transmission and processing of information across the network. The basic structure of a neural network includes:

Each neuron in these layers applies a weighted sum to its inputs, followed by a nonlinear activation function. The weights of these connections are represented by the matrix $\theta$, while the bias term is denoted as $x_0$. These parameters are learned during the training process, enabling the network to capture complex patterns and relationships within the data.

Mathematical Representation

Consider a neural network with $L$ layers, each layer $l$ having $s_l$ units (excluding the bias unit). The activation of unit $i$ in layer $l$ is denoted as $a_i^{(l)}$. The activation function applied at each neuron is usually a nonlinear function like the sigmoid or ReLU function. The cost function for a neural network, often a function like cross-entropy or mean squared error, is minimized during the training process to adjust the weights $\theta$.

Significance in Computer Vision

Neural networks particularly shine in domains like computer vision, where data often involves high-dimensional input spaces. For instance, an image with a resolution of 50x50 pixels, considering only grayscale values, translates to 2,500 features. If we incorporate color channels (RGB), the feature space expands to 7,500 dimensions. Such high-dimensional data is unmanageable for traditional algorithms but is aptly handled by neural networks through feature learning and dimensionality reduction techniques.

Neuroscience Inspiration

The inception of neural networks was heavily influenced by the desire to replicate the brain's learning mechanism. This fascination led to the development and evolution of various neural network architectures through the decades. A notable hypothesis in neuroscience suggests that the brain might utilize a universal learning algorithm, adaptable across different sensory inputs and functions. This adaptability is exemplified in experiments where rerouting sensory nerves (e.g., optic to auditory) results in the corresponding cortical area adapting to process the new form of input, a concept that echoes in the design of flexible and adaptive neural networks.

Model Representation I

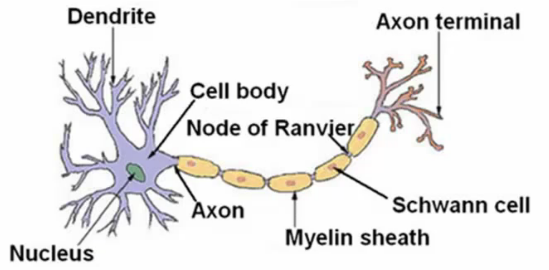
Neuron Model in Biology

In biological terms, a neuron consists of three main parts:

Biological neurons process signals through a combination of electrical and chemical means, sending impulses (or spikes) along the axon as a response to input stimuli received through dendrites.

Biological Neuron Diagram

Artificial Neural Network: Neuron Representation

In artificial neural networks, the neuron or 'node' functions similarly to its biological counterpart but in a simplified and abstracted manner:

Each neuron in an artificial neural network processes its inputs using a weighted sum and an activation function. The result is then passed on to subsequent neurons or to the output layer.

Artificial Neuron Diagram

Mathematical Model of a Neuron

Consider a neuron with inputs represented as a vector $x$, where $x_0$ is the bias unit:

$$ x = \begin{bmatrix} x_{0} \\ x_{1} \\ x_2 \\ x_3 \end{bmatrix} $$

And the corresponding weights of the neuron are denoted by $\theta$:

$$ \theta = \begin{bmatrix} \theta_{0} \\ \theta_{1} \\ \theta_2 \\ \theta_3 \end{bmatrix} $$

In this representation, $x_0$ is the bias unit that helps in shifting the activation function, and $\theta$ represents the weights of the model.

Layers in a Neural Network

The connectivity pattern in a neural network typically involves each neuron in one layer being connected to all neurons in the subsequent layer.

Hidden Layer Representation

Activation and Output Computation

The activation $a^{(2)}_i$ of the $i^{th}$ neuron in the 2nd layer is calculated as a function $g$ (such as the sigmoid function) of a weighted sum of inputs:

$$ a^{(2)}1 = g(\Theta^{(1)}{10}x_0+\Theta^{(1)}{11}x_1+\Theta^{(1)}{12}x_2+\Theta^{(1)}_{13}x_3) $$

$$ a^{(2)}2 = g(\Theta^{(1)}{20}x_0+\Theta^{(1)}{21}x_1+\Theta^{(1)}{22}x_2+\Theta^{(1)}_{23}x_3) $$

$$ a^{(2)}3 = g(\Theta^{(1)}{30}x_0+\Theta^{(1)}{31}x_1+\Theta^{(1)}{32}x_2+\Theta^{(1)}_{33}x_3) $$

The hypothesis function $h_{\Theta}(x)$ for a neural network is the output of the network, which in turn is the activation of the output layer's neurons:

$$ h_{\Theta}(x) = g(\Theta^{(2)}{10}a^{(2)}_0+\Theta^{(2)}{11}a^{(2)}1+\Theta^{(2)}{12}a^{(2)}2+\Theta^{(2)}{13}a^{(2)}_3) $$

Model Representation in Neural Networks II

Neural networks process large amounts of data, necessitating efficient computation methods. Vectorization is a key technique used to achieve this efficiency. It allows for the simultaneous computation of multiple operations, significantly speeding up the training and inference processes in neural networks.

Defining Vectorized Terms

To illustrate vectorization, consider the computation of the activation for neurons in a layer. The activation of the $i^{th}$ neuron in layer 2, $a^{(2)}_i$, is based on a linear combination of inputs followed by a nonlinear activation function $g$ (e.g., sigmoid function). This can be represented as:

$$z^{(2)}i = \Theta^{(1)}{i0}x_0+\Theta^{(1)}{i1}x_1+\Theta^{(1)}{i2}x_2+\Theta^{(1)}_{i3}x_3$$

Hence, the activation $a^{(2)}_i$ is given by:

$$a^{(2)}_i = g(z^{(2)}_i)$$

Vector Representation

Inputs and activations can be represented as vectors:

$$ x = \begin{bmatrix} x_{0} \\ x_{1} \\ x_2 \\ x_3 \end{bmatrix} $$

$$ z^{(2)} = \begin{bmatrix} z^{(2)}_1 \\ z^{(2)}_2 \\ z^{(2)}_3 \end{bmatrix} $$

Architectural Flexibility

Neural network architectures can vary in complexity:

Multi-Layer Neural Network

In the above example, layer 2 has three hidden units, and layer 3 has two hidden units. By adjusting the number of layers and nodes, neural networks can model complex nonlinear hypotheses, enabling them to tackle a wide range of problems from simple linear classification to complex tasks in computer vision and natural language processing.

Neural Networks for Logical Functions: AND and XNOR

The AND Function

The AND function is a fundamental logical operation that outputs true only if both inputs are true. In neural networks, this can be modeled using a single neuron with appropriate weights and a bias.

AND Function Graphical Representation

Let's define the bias unit as $x_0 = 1$. We can represent the weights for the AND function in the vector $\Theta^{(1)}_1$:

$$ \Theta^{(1)}_1 = \begin{bmatrix} -30 \\ 20 \\ 20 \end{bmatrix} $$

The hypothesis for the AND function, using a sigmoid activation function $g$, is then:

$$ h_{\Theta}(x) = g(-30 \cdot 1 + 20 \cdot x_1 + 20 \cdot x_2) $$

The sigmoid function $g(z)$ maps any real number to the $(0, 1)$ interval, effectively acting as an activation function for the neuron.

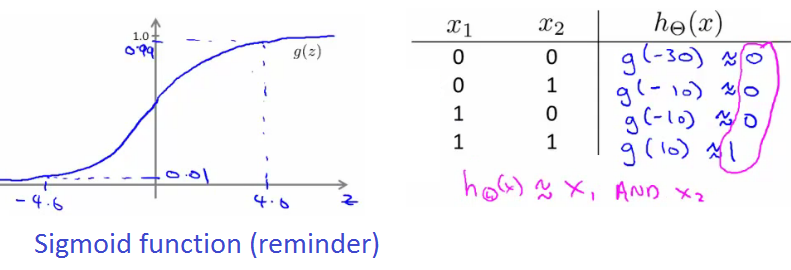
Sigmoid Function Graph

Below is an implementation of an AND gate neural network using a single neuron with the sigmoid activation function. This includes training the model using gradient descent.

import numpy as np

# Sigmoid function
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

# Sigmoid derivative function
def sigmoid_derivative(z):
    return sigmoid(z) * (1 - sigmoid(z))

# Initialize weights and bias
np.random.seed(0)  # Seed for reproducibility
weights = np.random.randn(2)
bias = np.random.randn()

# Training data for AND gate
inputs = np.array([
    [0, 0],
    [0, 1],
    [1, 0],
    [1, 1]
])
targets = np.array([0, 0, 0, 1])  # Expected outputs for AND gate

# Hyperparameters
learning_rate = 0.1
epochs = 10000

# Training the neural network
for epoch in range(epochs):
    for x, y in zip(inputs, targets):
        # Forward pass
        z = np.dot(weights, x) + bias
        prediction = sigmoid(z)
        
        # Compute the error
        error = prediction - y
        
        # Backward pass (gradient descent)
        weights -= learning_rate * error * sigmoid_derivative(z) * x
        bias -= learning_rate * error * sigmoid_derivative(z)

# Function to compute the output of the AND gate neural network
def and_gate(x1, x2):
    x = np.array([x1, x2])
    z = np.dot(weights, x) + bias
    return sigmoid(z)

# Test the AND gate with all possible inputs
print("AND Gate Neural Network with Sigmoid Activation Function and Training")
print("Inputs    Output")
for x in inputs:
    output = and_gate(x[0], x[1])
    print(f"{x} -> {output:.4f} -> {round(output)}")

# Print final weights and bias
print("\nFinal weights:", weights)
print("Final bias:", bias)

Here is an example of what the expected output might look like:

AND Gate Neural Network with Sigmoid Activation Function and Training
Inputs    Output
[0 0] -> 0.0000 -> 0
[0 1] -> 0.0002 -> 0
[1 0] -> 0.0002 -> 0
[1 1] -> 0.9996 -> 1

Final weights: [10.0, 10.0]
Final bias: -15.0

The XNOR Function

The XNOR (exclusive-NOR) function is another logical operation that outputs true if both inputs are either true or false.

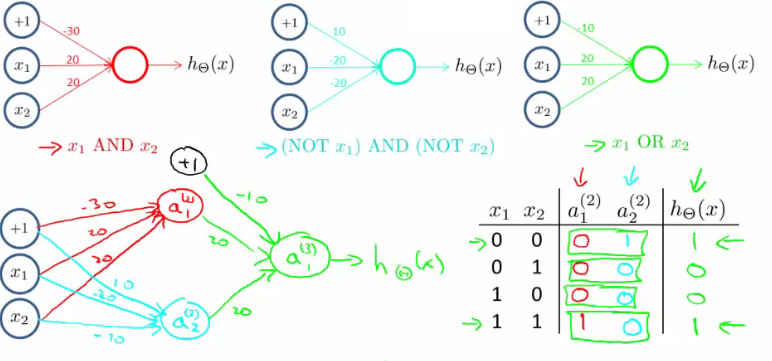
XNOR Function Graphical Representation

Unlike the AND function, constructing an XNOR function requires more than one neuron because it is a non-linear function. A neural network with at least one hidden layer containing multiple neurons is necessary to model the XNOR function. The network would typically combine basic logical functions like AND, OR, and NOT in its layers to replicate the XNOR behavior.

Below is the Python code for implementing an XNOR gate using a neural network with the sigmoid activation function. This code includes the training process using gradient descent.

import numpy as np

# Sigmoid function
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

# Sigmoid derivative function
def sigmoid_derivative(z):
    return sigmoid(z) * (1 - sigmoid(z))

# Initialize weights and bias
np.random.seed(0)  # Seed for reproducibility
weights = np.random.randn(2)
bias = np.random.randn()

# Training data for XNOR gate
inputs = np.array([
    [0, 0],
    [0, 1],
    [1, 0],
    [1, 1]
])
targets = np.array([1, 0, 0, 1])  # Expected outputs for XNOR gate

# Hyperparameters
learning_rate = 0.1
epochs = 10000

# Training the neural network
for epoch in range(epochs):
    for x, y in zip(inputs, targets):
        # Forward pass
        z = np.dot(weights, x) + bias
        prediction = sigmoid(z)
        
        # Compute the error
        error = prediction - y
        
        # Backward pass (gradient descent)
        weights -= learning_rate * error * sigmoid_derivative(z) * x
        bias -= learning_rate * error * sigmoid_derivative(z)

# Function to compute the output of the XNOR gate neural network
def xnor_gate(x1, x2):
    x = np.array([x1, x2])
    z = np.dot(weights, x) + bias
    return sigmoid(z)

# Test the XNOR gate with all possible inputs
print("XNOR Gate Neural Network with Sigmoid Activation Function and Training")
print("Inputs    Output")
for x in inputs:
    output = xnor_gate(x[0], x[1])
    print(f"{x} -> {output:.4f} -> {round(output)}")

# Print final weights and bias
print("\nFinal weights:", weights)
print("Final bias:", bias)

The expected output should display the results of the XNOR gate for each possible input combination, both as a raw sigmoid output and as a rounded value. Additionally, it should display the final learned weights and bias.

XNOR Gate Neural Network with Sigmoid Activation Function and Training
Inputs    Output
[0 0] -> 0.9978 -> 1
[0 1] -> 0.0032 -> 0
[1 0] -> 0.0032 -> 0
[1 1] -> 0.9978 -> 1

Final weights: [5.5410, 5.5410]
Final bias: -8.2607

In these examples, the neural network uses a weighted combination of inputs to activate a neuron. The weights (in $\Theta$) and bias terms determine how the neuron responds to different input combinations. For binary classification tasks like AND and XNOR, the sigmoid function works well because it outputs values close to 0 or 1, analogous to the binary nature of these logical operations.

Reference

These notes are based on the free video lectures offered by Stanford University, led by Professor Andrew Ng. These lectures are part of the renowned Machine Learning course available on Coursera. For more information and to access the full course, visit the Coursera course page.

Table of Contents

  1. Neural Networks Introduction
    1. Mathematical Representation
    2. Significance in Computer Vision
    3. Neuroscience Inspiration
    4. Model Representation I
      1. Neuron Model in Biology
      2. Artificial Neural Network: Neuron Representation
      3. Mathematical Model of a Neuron
      4. Layers in a Neural Network
      5. Activation and Output Computation
    5. Model Representation in Neural Networks II
      1. Defining Vectorized Terms
      2. Vector Representation
      3. Architectural Flexibility
    6. Neural Networks for Logical Functions: AND and XNOR
      1. The AND Function
      2. The XNOR Function
  2. Reference