Last modified: May 28, 2024

This article is written in: 🇺🇸

Recommendation Systems

Recommendation systems are a fundamental component in the interface between users and large-scale content providers like Amazon, eBay, and iTunes. These systems personalize user experiences by suggesting products, movies, or content based on past interactions and preferences.

Concept of Recommender Systems

• Purpose: To recommend new content or products to users based on their historical interactions or preferences.
• Nature: Not a single algorithm, but a category of methods tailored to predicting user preferences.

Example Scenario: Movie Rating Prediction

Imagine a company that sells movies and allows users to rate them. Consider the following setup:

• Movies: A catalog of five movies.
• Users: A database of four users.
• User Ratings: Users rate movies on a scale of 1 to 5.

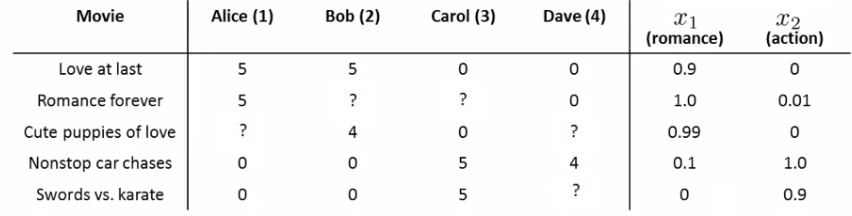
Notations:

• $n_u$: Number of users.
• $n_m$: Number of movies.
• $r(i, j)$: Indicator (1 or 0) if user $j$ has rated movie $i$.
• $y^{(i, j)}$: Rating given by user $j$ to movie $i$.

Feature Vectors and Parameter Vectors

• Movie Features: Each movie can have a feature vector representing various attributes or genres.
• Additional Feature (x0 = 1): For computational convenience, an additional feature is added to each movie's feature vector.

Example for "Cute Puppies of Love":

$$ x^{(3)} = \begin{bmatrix} 1 \\ 0.99 \\ 0 \end{bmatrix} $$

• User Parameters: Each user has a parameter vector representing their preferences.

Example for user 1 (Alice) and her preference for "Cute Puppies of Love":

$$ \theta^{(1)} = \begin{bmatrix} 0 \\ 5 \\ 0 \end{bmatrix} $$

Example Scenario: Movie Rating Prediction

Imagine a company that sells movies and allows users to rate them. Consider the following setup:

• Movies: A catalog of five movies.
• Users: A database of four users.
• User Ratings: Users rate movies on a scale of 1 to 5.

Notations:

• $n_u$: Number of users.
• $n_m$: Number of movies.
• $r(i, j)$: Indicator (1 or 0) if user $j$ has rated movie $i$.
• $y^{(i, j)}$: Rating given by user $j$ to movie $i$.

Feature Vectors and Parameter Vectors

• Movie Features: Each movie can have a feature vector representing various attributes or genres.
• Additional Feature ($x_0 = 1$): For computational convenience, an additional feature is added to each movie's feature vector.

Example for "Cute Puppies of Love":

$$ x^{(3)} = \begin{bmatrix} 1 \\ 0.99 \\ 0 \end{bmatrix} $$

• User Parameters: Each user has a parameter vector representing their preferences.

Example for user 1 (Alice) and her preference for "Cute Puppies of Love":

$$ \theta^{(1)} = \begin{bmatrix} 0 \\ 5 \\ 0 \end{bmatrix} $$

Mock Implementation in Python

This implementation demonstrates how to set up a basic collaborative filtering model for movie rating prediction using Python.

Step 1: Data Setup

import numpy as np

# Number of users and movies
n_u = 4
n_m = 5

# User ratings matrix (0 if not rated)
ratings = np.array([
    [5, 4, 0, 0, 3],
    [0, 0, 4, 0, 4],
    [0, 0, 5, 3, 3],
    [3, 4, 0, 0, 5]
])

# Indicator matrix r(i, j) = 1 if rated, 0 otherwise
R = (ratings != 0).astype(int)

Step 2: Feature and Parameter Initialization

# Initialize random movie feature vectors (3 features per movie)
X = np.random.rand(n_m, 3)

# Initialize random user parameter vectors (3 parameters per user)
Theta = np.random.rand(n_u, 3)

Step 3: Collaborative Filtering Cost Function

def collaborative_filtering_cost(X, Theta, ratings, R, lambda_ = 0.1):
    predictions = X.dot(Theta.T)
    error = (predictions - ratings) * R
    cost = 0.5 * np.sum(error**2)
    
    # Regularization
    cost += (lambda_ / 2) * (np.sum(Theta**2) + np.sum(X**2))
    
    return cost

cost = collaborative_filtering_cost(X, Theta, ratings, R)
print(f'Initial cost: {cost}')

Step 4: Gradient Descent for Optimization

def collaborative_filtering_gradient(X, Theta, ratings, R, alpha=0.01, lambda_ = 0.1, iterations=1000):
    X_grad = np.zeros(X.shape)
    Theta_grad = np.zeros(Theta.shape)
    
    for _ in range(iterations):
        predictions = X.dot(Theta.T)
        error = (predictions - ratings) * R
        
        X_grad = error.dot(Theta) + lambda_ * X
        Theta_grad = error.T.dot(X) + lambda_ * Theta
        
        X -= alpha * X_grad
        Theta -= alpha * Theta_grad
        
        cost = collaborative_filtering_cost(X, Theta, ratings, R, lambda_)
        if _ % 100 == 0:
            print(f'Iteration {_}: cost = {cost}')
    
    return X, Theta

X, Theta = collaborative_filtering_gradient(X, Theta, ratings, R)

Making Predictions

To predict how much Alice might like "Cute Puppies of Love", we compute:

$$ (\theta^{(1)})^T x^{(3)} = (0 \cdot 1) + (5 \cdot 0.99) + (0 \cdot 0) = 4.95 $$

This predicts a high rating of 4.95 out of 5 for Alice for this movie, based on her preference parameters and the movie's features.

Here is an example implementation in Python:

import numpy as np

# Feature vector for the movie "Cute Puppies of Love"
x_cute_puppies = np.array([1, 0.99, 0])

# Parameter vector for Alice
theta_alice = np.array([0, 5, 0])

# Compute the dot product
predicted_rating = np.dot(theta_alice, x_cute_puppies)

# Print the predicted rating
print(f"Predicted rating for Alice for 'Cute Puppies of Love': {predicted_rating}")

When you run this code, it will output:

Predicted rating for Alice for 'Cute Puppies of Love': 4.95

Collaborative Filtering

• Method: Collaborative filtering is often used in recommender systems. It involves learning either user preferences or item features, depending on the data available.
• Learning: This can be achieved using algorithms like gradient descent.
• Advantage: The system can learn to make recommendations on its own without explicit programming of the features or preferences.

Learning User Preferences in Recommendation Systems

In recommendation systems, learning user preferences $(\theta^j)$ is a key component. This process is akin to linear regression, but with a unique approach tailored for recommendation contexts.

Minimizing Cost Function for User Preferences

• The objective is to minimize the following cost function for each user $j$:

$$ \min_{\theta^j} = \frac{1}{2m^{(j)}} \sum_{i:r(i,j)=1} \left((\theta^{(j)})^T(x^{(i)}) - y^{(i,j)}\right)^2 + \frac{\lambda}{2m^{(j)}} \sum_{k=1}^{n} (\theta_k^{(j)})^2 $$

• Here, $m^{(j)}$ is the number of movies rated by user $j$, $\lambda$ is the regularization parameter, and $r(i, j)$ indicates whether user $j$ has rated movie $i$.

Gradient Descent for Optimization

Update Rule for $\theta_k^{(j)}$:

• For $k = 0$ (bias term):

$$ \theta_k^{(j)} := \theta_k^{(j)} - \alpha \sum_{i:r(i,j)=1} \left((\theta^{(j)})^T(x^{(i)}) - y^{(i,j)}\right) x_k^{(i)} $$

• For $k \neq 0$:

$$ \theta_k^{(j)} := \theta_k^{(j)} - \alpha \left(\sum_{i:r(i,j)=1} \left((\theta^{(j)})^T(x^{(i)}) - y^{(i,j)}\right) x_k^{(i)} + \lambda \theta_k^{(j)}\right) $$

Collaborative Filtering Algorithm

Collaborative filtering leverages the interplay between user preferences and item (movie) features:

• Learning Features from Preferences: Given user preferences $(\theta^{(1)}, ..., \theta^{(n_u)})$, the algorithm can learn movie features $(x^{(1)}, ..., x^{(n_m)})$.
• Cost Function for Movies:

$$ \min_{x^{(1)}, ..., x^{(n_m)}} \frac{1}{2} \sum_{i=1}^{n_m} \sum_{i:r(i,j)=1} \left((\theta^{(j)})^T(x^{(i)}) - y^{(i,j)}\right)^2 + \frac{\lambda}{2} \sum_{i=1}^{n_m} \sum_{k=1}^{n} (x_k^{(i)})^2 $$

• Iterative Process: The algorithm typically involves an iterative process, alternating between optimizing for movie features and user preferences.

Collaborative Filtering Implementation

Here, we'll implement a basic collaborative filtering model using gradient descent to predict user ratings for movies.

Step 1: Data Setup

First, we need to set up our data, including user ratings and an indicator matrix showing which movies have been rated by which users.

import numpy as np

# Number of users and movies
n_u = 4
n_m = 5

# User ratings matrix (0 if not rated)
ratings = np.array([
    [5, 4, 0, 0, 3],
    [0, 0, 4, 0, 4],
    [0, 0, 5, 3, 3],
    [3, 4, 0, 0, 5]
])

# Indicator matrix r(i, j) = 1 if rated, 0 otherwise
R = (ratings != 0).astype(int)

Step 2: Feature and Parameter Initialization

We initialize random feature vectors for movies and parameter vectors for users.

# Initialize random movie feature vectors (3 features per movie)
X = np.random.rand(n_m, 3)

# Initialize random user parameter vectors (3 parameters per user)
Theta = np.random.rand(n_u, 3)

Step 3: Collaborative Filtering Cost Function

We define the cost function for collaborative filtering, including regularization.

def collaborative_filtering_cost(X, Theta, ratings, R, lambda_=0.1):
    predictions = X.dot(Theta.T)
    error = (predictions - ratings) * R
    cost = 0.5 * np.sum(error ** 2)
    
    # Regularization
    cost += (lambda_ / 2) * (np.sum(Theta ** 2) + np.sum(X ** 2))
    
    return cost

cost = collaborative_filtering_cost(X, Theta, ratings, R)
print(f'Initial cost: {cost}')

Step 4: Gradient Descent for Optimization

We implement gradient descent to optimize the feature and parameter vectors.

def collaborative_filtering_gradient(X, Theta, ratings, R, alpha=0.01, lambda_=0.1, iterations=1000):
    for _ in range(iterations):
        predictions = X.dot(Theta.T)
        error = (predictions - ratings) * R
        
        X_grad = error.dot(Theta) + lambda_ * X
        Theta_grad = error.T.dot(X) + lambda_ * Theta
        
        X -= alpha * X_grad
        Theta -= alpha * Theta_grad
        
        if _ % 100 == 0:
            cost = collaborative_filtering_cost(X, Theta, ratings, R, lambda_)
            print(f'Iteration {_}: cost = {cost}')
    
    return X, Theta

X, Theta = collaborative_filtering_gradient(X, Theta, ratings, R)

Step 5: Prediction

Finally, we use the optimized feature and parameter vectors to predict ratings for all users and movies.

# Predict ratings for all users and movies
predictions = X.dot(Theta.T)

# Print predictions
print("Predicted ratings:")
print(predictions)

Vectorization: Low Rank Matrix Factorization

• Matrix Y: Organize all user ratings into a matrix Y, which represents the interactions between users and movies.

Example $[5 \times 4]$ Matrix Y for 5 movies and 4 users:

$$ Y = \begin{pmatrix} 5 & 5 & 0 & 0 \\ 5 & ? & ? & 0 \\ ? & 4 & 0 & ? \\ 0 & 0 & 5 & 4 \\ 0 & 0 & 5 & 0 \end{pmatrix} $$

• Predicted Ratings Matrix: The predicted ratings can be expressed as the product of matrices $X$ and $\Theta^T$.

$$ X \Theta^T = \begin{pmatrix} (\theta^{(1)})^T(x^{(1)}) & \dots & (\theta^{(n_u)})^T(x^{(1)}) \\ \vdots & \ddots & \vdots \\ (\theta^{(1)})^T(x^{(n_m)}) & \dots & (\theta^{(n_u)})^T(x^{(n_m)}) \end{pmatrix} $$

• Matrix X: Contains the features for each movie, stacked in rows.
• Matrix $\Theta$: Contains the user preferences, also stacked in rows.

Low Rank Matrix Factorization Example Implementation

To implement the low-rank matrix factorization for collaborative filtering, we need to set up the necessary matrices and perform the matrix multiplication to predict ratings. Here's how to do it in Python.

Step 1: Define the Matrix Y

Organize all user ratings into a matrix $Y$, which represents the interactions between users and movies.

import numpy as np

# Example [5 x 4] Matrix Y for 5 movies and 4 users
Y = np.array([
    [5, 5, 0, 0],
    [5, 0, 0, 0],
    [0, 4, 0, 0],
    [0, 0, 5, 4],
    [0, 0, 5, 0]
])

print("Matrix Y:")
print(Y)

Step 2: Initialize Matrices X and Θ

Matrix $X$ contains the features for each movie, and matrix $\Theta$ contains the user preferences.

# Number of movies (n_m) and users (n_u)
n_m, n_u = Y.shape

# Number of features
n_features = 3

# Initialize movie feature matrix X and user preference matrix Theta with random values
X = np.random.rand(n_m, n_features)
Theta = np.random.rand(n_u, n_features)

print("\nInitial Matrix X (Movie Features):")
print(X)

print("\nInitial Matrix Θ (User Preferences):")
print(Theta)

Step 3: Compute the Predicted Ratings Matrix

The predicted ratings matrix can be expressed as the product of matrices $X$ and $\Theta^T$.

# Compute the predicted ratings
predicted_ratings = X.dot(Theta.T)

print("\nPredicted Ratings Matrix XΘ^T:")
print(predicted_ratings)

This Python code demonstrates the setup of matrices $Y$, $X$, and $\Theta$, and the calculation of the predicted ratings matrix using matrix multiplication. The matrix $X$ contains the features for each movie, and $\Theta$ contains the user preferences. The predicted ratings matrix is obtained by multiplying $X$ with the transpose of $\Theta$.

Scenario: A User with No Ratings

Imagine a user in a movie recommendation system who hasn't rated any movies. This scenario presents a challenge for typical collaborative filtering algorithms.

• For such a user, there are no movies for which $r(i, j) = 1$.
• As a result, the algorithm ends up minimizing only the regularization term for this user, which doesn't provide meaningful insight for recommendations.

Mean Normalization Approach

1. Compute the Mean Rating: Calculate the average rating for each movie and store these in a vector $\mu$.

Example $\mu$ vector for a system with 5 movies:

$$ \mu = \begin{bmatrix} 2.5 \\ 2.5 \\ 2 \\ 2.25 \\ 1.25 \end{bmatrix} $$

1. Normalize the Ratings Matrix: Subtract the mean rating for each movie from all its ratings in the matrix $Y$.

Normalized Ratings Matrix $Y$:

$$ Y = \begin{pmatrix} 2.5 & 2.5 & -2.5 & -2.5 & ? \\ 2.5 & ? & ? & -2.5 & ? \\ ? & 2 & -2 & ? & ? \\ -2.25 & -2.25 & 2.75 & 1.75 & ? \\ -1.25 & -1.25 & 3.75 & -1.25 & ? \end{pmatrix} $$

1. Adjust for Users with No Ratings: For a new user with no ratings, their predicted rating for each movie can be initialized to the mean rating of that movie. This provides a baseline from which personalized recommendations can evolve as the user starts rating movies.

Scenario: A User with No Ratings

Imagine a user in a movie recommendation system who hasn't rated any movies. This scenario presents a challenge for typical collaborative filtering algorithms.

For such a user, there are no movies for which $r(i, j) = 1$. As a result, the algorithm ends up minimizing only the regularization term for this user, which doesn't provide meaningful insight for recommendations.

Mean Normalization Approach

1. Compute the Mean Rating: Calculate the average rating for each movie and store these in a vector $\mu$.

Example $\mu$ vector for a system with 5 movies:

$$ \mu = \begin{bmatrix} 2.5 \\ 2.5 \\ 2 \\ 2.25 \\ 1.25 \end{bmatrix} $$

1. Normalize the Ratings Matrix: Subtract the mean rating for each movie from all its ratings in the matrix $Y$.

Normalized Ratings Matrix $Y$:

$$ Y = \begin{pmatrix} 2.5 & 2.5 & -2.5 & -2.5 & ? \\ 2.5 & ? & ? & -2.5 & ? \\ ? & 2 & -2 & ? & ? \\ -2.25 & -2.25 & 2.75 & 1.75 & ? \\ -1.25 & -1.25 & 3.75 & -1.25 & ? \end{pmatrix} $$

1. Adjust for Users with No Ratings: For a new user with no ratings, their predicted rating for each movie can be initialized to the mean rating of that movie. This provides a baseline from which personalized recommendations can evolve as the user starts rating movies.

Implementation in Python

Step 1: Define the Matrix Y and Compute Mean Ratings

import numpy as np

# Example [5 x 4] Matrix Y for 5 movies and 4 users
Y = np.array([
    [5, 5, 0, 0],
    [5, 0, 0, 0],
    [0, 4, 0, 0],
    [0, 0, 5, 4],
    [0, 0, 5, 0]
])

# Compute the mean rating for each movie, ignoring zeros
mean_ratings = np.true_divide(Y.sum(1), (Y != 0).sum(1))

print("Mean Ratings Vector μ:")
print(mean_ratings)

Step 2: Normalize the Ratings Matrix

# Subtract the mean rating for each movie from all its ratings
Y_normalized = Y - mean_ratings[:, np.newaxis]
# Ensure we do not subtract from places where rating was 0
Y_normalized[Y == 0] = 0

print("\nNormalized Ratings Matrix Y:")
print(Y_normalized)

Step 3: Adjust for Users with No Ratings

For a new user with no ratings, their predicted rating for each movie can be initialized to the mean rating of that movie.

# Predicted ratings for a new user with no ratings
new_user_ratings = mean_ratings.copy()

print("\nPredicted Ratings for New User with No Ratings:")
print(new_user_ratings)

Benefits of Mean Normalization

• Handling New Users: Provides a starting point for recommendations for users who have not yet provided any ratings.
• Rating Sparsity: Mitigates issues arising from sparse data, which is common in many real-world recommendation systems.
• Balancing the Dataset: Normalization helps in balancing the dataset, especially when there are variations in the number of ratings per movie.

Reference

These notes are based on the free video lectures offered by Stanford University, led by Professor Andrew Ng. These lectures are part of the renowned Machine Learning course available on Coursera. For more information and to access the full course, visit the Coursera course page.